GRADIENT DESCENT ALGORITHM
When one start Learning For Machine Learning, As a beginner one founds a very complex explanation of Gradient Descent Algorithm and since it is a very important algorithm in machine Learning,understanding it, is also much important. Today , in this article we will try to understand Gradient Descent in very easy, brief and well explained way.
Gradient Descent is the most common optimization algorithm in machine learning and deep learning. It is a first-order optimization algorithm. This means it only takes into account the first derivative when performing the updates on the parameters.
If we start searching for Gradient Descent Algorithm ,we found this picture.
Don't panic! Let me explain you
z is a cost function of x and y.We have to find those value of x and y for which value of cost function (z) is minimum.
If we visualize it, splitted in two part (z VS x for any fix value of y) and (z VS y for any fix value of x) it looks easier.

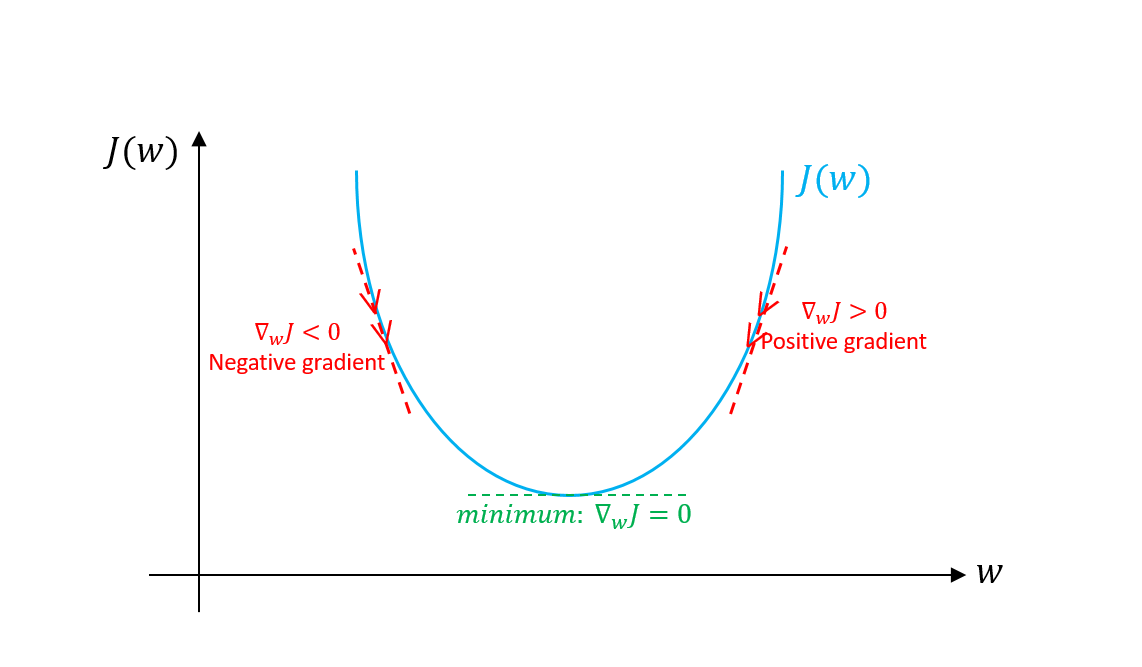
From Above graphs, It is quite clear that if we go opposite to the slope from any point, we will tend toward minima point.
But now what matters is, how much distance we'll take in single step, If we take a quite big step in opposite direction, we may cross the minima point.
Gradient Descent is the most common optimization algorithm in machine learning and deep learning. It is a first-order optimization algorithm. This means it only takes into account the first derivative when performing the updates on the parameters.
If we start searching for Gradient Descent Algorithm ,we found this picture.
Don't panic! Let me explain you
z is a cost function of x and y.We have to find those value of x and y for which value of cost function (z) is minimum.
If we visualize it, splitted in two part (z VS x for any fix value of y) and (z VS y for any fix value of x) it looks easier.

Gradient Descent Algorithm provides an efficient way to find the optimum value of y and x (or all the features on which cost function depends), which will minimize the value of cost function(z).
Points to Know Before Proceeding:
- This is an iterative method ,you would have familiarity with iterative method(If not, no need to panic).Iterative method is which,where we start with pre-assumed value of any variable and iterate over it,find new values and get closer to desired value
- From any point, if we go opposite direction of slope,we will tend toward minima of that region.This is the key behind Gradient descent algorithm.If I plot above two graphs again with arrow direction, you'll understand.
From Above graphs, It is quite clear that if we go opposite to the slope from any point, we will tend toward minima point.
But now what matters is, how much distance we'll take in single step, If we take a quite big step in opposite direction, we may cross the minima point.
Fig: Jump Over minima
- The Step size is quantified by a variable called 'learning rate(η)'. We choose a value of 'η' such that, while iterating, we don't jump over the minima .It is generally taken 0.001(we can change it depends upon data-set given)
Finally the iterating formula for Gradient Descent Algorithm:
(y)new=(y)old - η*(∂j/∂y)
(x)new=(x)old - η*(∂j/∂x)
In General:
(θ)new=(θ)old - η*∇θ
Where θ = [θ1,θ2, ... ,θn]
∇θ = Gradient of θ= [∂z/∂θ1,∂z/∂θ2, ... ,∂z/∂θn]
Above is Called Gradient Descent Algorithm. In next post, we will discuss about implementation of it.We will try to understand Linear Regression ( fitting a line to given dataset ) using Gradient Descent.
If You have any doubt , Ask us in comment. Also u can mail us at 4wallspace@gmail.com





Comments
Post a Comment