Skip to main content

Linear Regression(With Gradient Descent ) Fully Explained| Machine Learning

Linear Regression (Gradient Descent Method)

If you don't have any idea of Gradient Descent Algorithm, please check our previous post, there I have explained Gradient Descent Algorithm very well explained in brief.

Now moving toward our current topic Linear Regression . In the previous post , we have just discussed the theory behind the Gradient Descent. Today we will learn Linear Regression where we will use Gradient Descent to minimize the cost function.

WHAT IS LINEAR REGRESSION:

Suppose you are given a equation: y=2x1+3x2+4x3+1 and you are said to find the value at any point (1,1,1) corresponds to x1, x2, x3 respectively.
You'll simply put the value of x1, x2, x3 into equation and tell me the answer :10,Right?
But What if you are given different set of (x1, x2, x3,y) and you are said to find the equation.
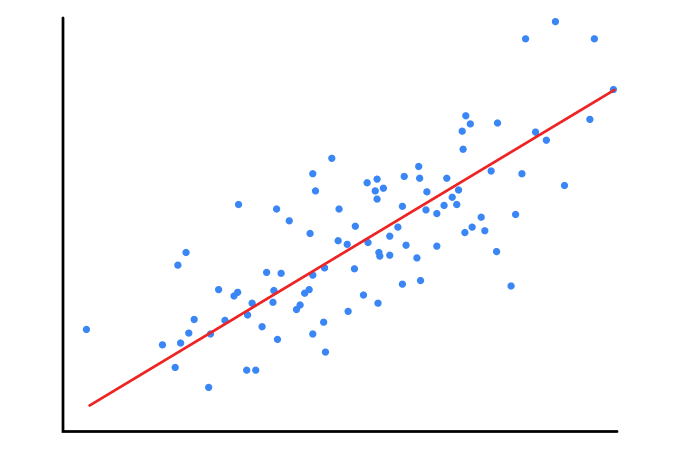
Here's what,Linear Regression Comes into picture.It helps us to find out or fit a Linear equation to datasets  given.

Above equation can be easily transformed to following form.If we suppose:
θ=[2,3,4]
X=[x1, x2, x3]
c=1
Above equation can be written as : Y=θ.X+C
Linear Regression help us to find the value of θ and c
For this post we will be limited to a single line equation, multidimensional linear equation can also be done in similar way.
X      Y
2      7
3    10
4    13
5    16
After Seeing above data set, we can clearly say ,there is a relation ,
Y=2*X +1
is there.But how will we get above equation using linear regression , will try to understand in this post.
  •  Assume a line yp=mx+c
  • Cost Function : Our cost function is Measured Squared Error(MSE) i.e Average squared difference of observed value and predicted value.
Cost Function=Mean Squared Error(MSE) = (1/n)Σ(y - yp)2
J(m,c) = (1/n)Σ(y-(mx+c))2

J(m,c) is our cost function now which depends on m and c, as z was depending upon x and y in post of gradient descent.
Now,
For Gradient Descent we need:

∂j/∂m=(-2/n)Σ(x*(y-(mx+c)))

∂j/∂c=(-2/n)Σ(y-(mx+c))

Assume,

learning_rate(η) =0.001

Iterations:

(m)new=(m)old - η*(∂j/∂m)

(c)new=(c)old - η*(∂j/∂c)


How many times you want to iterate? It depends upon you or you can fix a condition like cost<=0.000001

Try Below given Code:

Python Code to implement this






Labels:

Comments

Post a Comment

Popular posts from this blog

Perceptron Algorithm | Pegasos Algorithm | Support Vector Machine | Linear Classifier Among Dataset | Deep Learning | Machine Learning

PERCEPTRON ALGORITHM Perceptron Algorithm is one of the most used algorithm in classifying data.It frequently seems little tough while learning first time. In today's post , We'll try to understand it well in brief with full explanation.  Perceptron Algorithm is used whenever given dataset can be classified into two parts or it has only two labels.(One can consider it as +1, -1) There are three version of Perceptron Algorithm: Simple Perceptron  Average Percepron Pegasos Algorithm or Support Vector  Machine Relax! Terms are sounding dangerous but they are really very easy.Let me explain you. 1.Simple Perceptron: The single target of perceptron algorithm is to find a Linear classifier( say Linear equation) on one side of which are all positively labelled point and on another side all negatively labelled points are there. As we know any linear equation can be written as, Y= θ .X + θ 0 Using Perceptron Our Aim is to find those value of θ vec...
Post a Comment
Read more

Gradient Descent Algorithm Fully Explained| Machine Learning

GRADIENT DESCENT ALGORITHM When one start Learning For Machine Learning, As a beginner one founds a very complex explanation of Gradient Descent Algorithm and since it is a very important algorithm in machine Learning,understanding it, is also much important. Today , in this article we will try to understand Gradient Descent   in very easy, brief and well explained way. Gradient Descent  is the most common optimization algorithm in  machine learning  and  deep learning . It is a first-order optimization algorithm. This means it only takes into account the first derivative when performing the updates on the parameters. If we start searching for Gradient Descent Algorithm ,we found this picture. Don't panic! Let me explain you z is a cost function of x and y.We have to find those value of x and y for which value of cost function (z) is minimum. If we visualize it, splitted in two part (z VS x for any fix value of y) and (z VS y for any fix value ...
Post a Comment
Read more

Stochastic Gradient Descent Algorithm Fully Explained | Machine Learning

STOCHASTIC GRADIENT DESCENT STOCHASTIC GRADIENT DESCENT  is an efficient algorithm over GRADIENT DESCENT when it requires to deal with BIG DATA.Where Data are huge STOCHASTIC GRADIENT DESCENT is used. In our Previous post, We already discussed about GRADIENT DESCENT ( Click Here ) very well.In this post, we will try to understand STOCHASTIC GRADIENT DESCENT.  Both are almost same , only difference comes while iterating: In Gradient Descent ,We had four things Feature Vector(X) Label(Y) Cost function(J) Predicted Value( Y p) θ was representing the coefficient/Weightage vector for feature vector,  θ 0   Offset Parameter Y p =θ.X+θ 0 θ new =θ old -(η*∂J/∂θ) The Single Difference between Gradient Descent and Stochastic Gradient Descent comes while iterating: In Gradient Descent ,   We sum up the losses over all the data points given and take average in our cost function, Something like this: J=(1/n)ΣLoss(Y i ,Y p i ) ∂J/∂θ=(1...
Post a Comment
Read more